立体図形の切断（灘中）[S-0015-R]

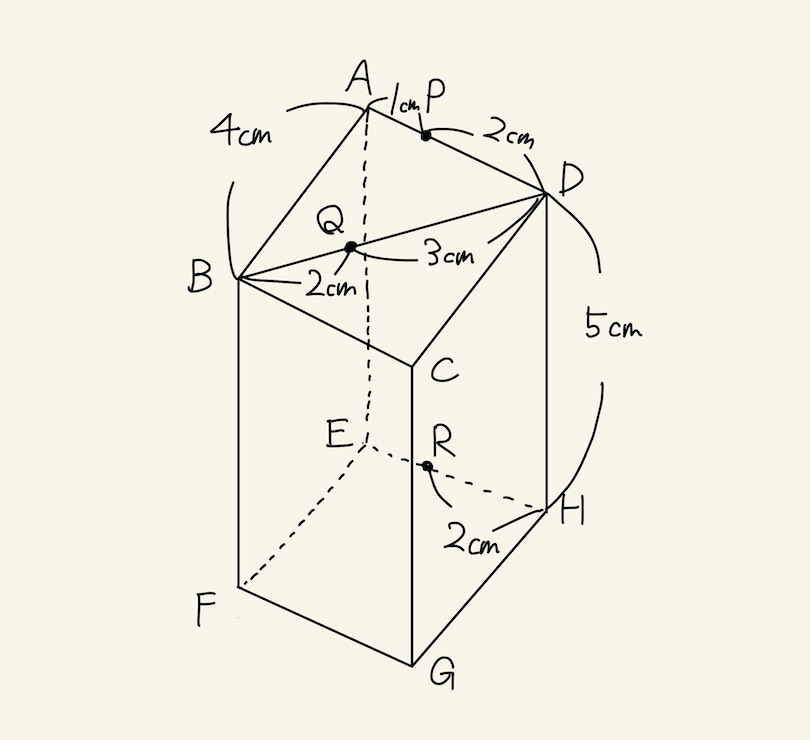
上の図のように、直方体ABCDーEFGHと3点P,Q,Rがあります。3点B,D,Hを通る平面をア、3点P,Q,Rを通る平面をイ、3点A,B,Hを通る平面をウとします。

この直方体を平面アとイで切って、4つの立体に分けるとき、頂点Eを含む立体の体積は（　　　①　　　）cm³です。

また、この直方体を平面ア、イ、ウで切って、8つの立体に分けるとき、頂点Eを含む立体の体積は（　　　②　　　）cm³です。

まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。（※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。）

その後（解き終えたら、または目安時間が経過したら）、下にスクロールして解説（思考の例）をじっくり読んでください。

ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ（クリティカルシンキング）を鍛えることが今回の目的です。

クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう！

1.目的は何かを常に意識する。
（何を問われているのか？どんな理解を試されているのか？など題意を見抜く。）

• これは特にひねりもなく、切断面と切断後の立体の形が正確に把握できるかどうかの問題だな。
• 縦方向、横方向、高さ方向に分けて、しっかりと切断面がどこの点を通るのかを把握しよう。

このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。

2.前提条件、置かれた環境に合わせて考える。
（思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。）

• 立体の形に注意し、あとは相似などを使えば良いだろう。

ここでは思い込を排除し、事実だけを書き入れて整理することが大切です。

3.目的を踏まえたうえで、「考える枠組み」を考える。
（どんな項目について考えればゴールに到着するかの見当をつける。）

• とにかく、切断面を正確に。

ここでは考える方向性だけに集中しましょう。

4.構造的にアプローチする。
（抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。）

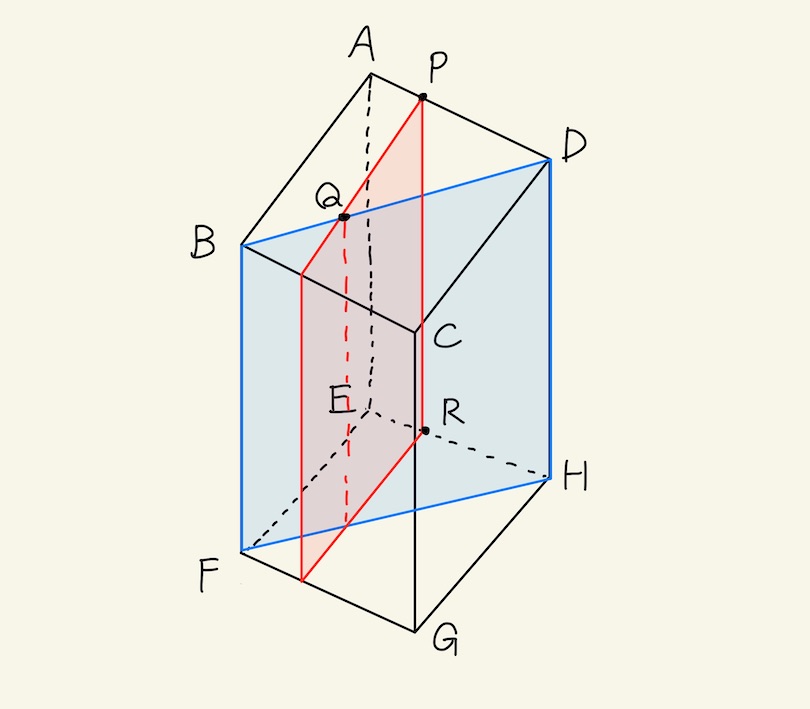
• B、D、Hと通るということは、BDの角度を保ったまま、D→F高さ方向に垂直に切断するので、Fを通ることになる。
• アの切断面は上記の図の青色ようになる。
• P、Q、Rと通るということは、PQの角度を保ったまま、P→R高さ方向に垂直に切断する。
• イの切断面は上記の図の赤色ようになる。
• ①で求める体積は底面が四角形ABQP、高さがBFの四角柱と分かる。
• 底面積（ABQP）は、辺の比から分かる。
• DA:DP=3:2
• DB:DQ=5:3
• △DAB - △DPQ ＝(4 × 3 × 1/2 ) - (4 × 3 × 1/2 ) × 2/3 × 3/5 = 6 - 12/5 = 18/5 cm²
• ① = 18/5 × 5 = 18 cm²

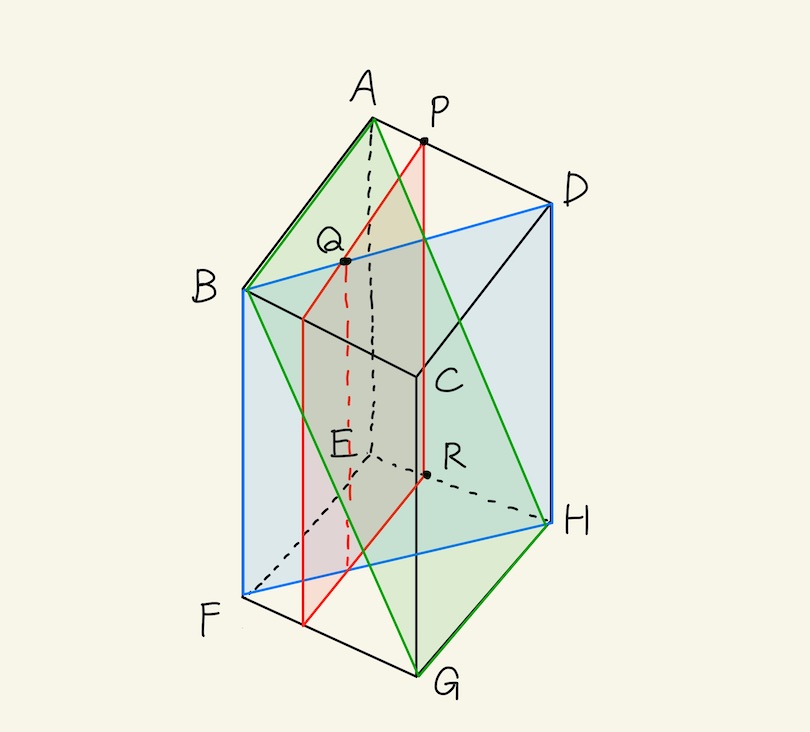
• 続いて、ウでの切断が加わると上記の図（緑面）のようになる。

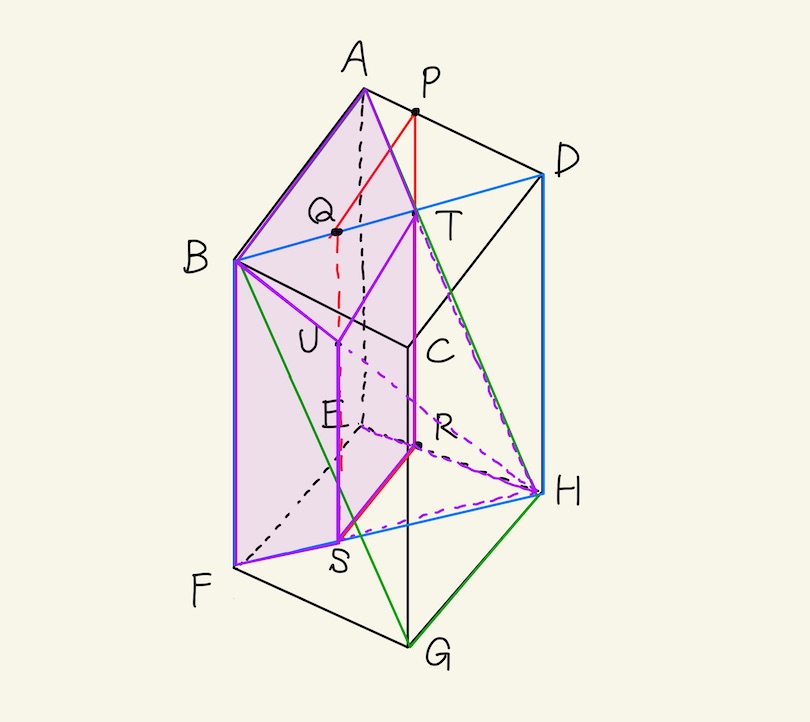
• 切断の順序を工夫する！
• ①を②の誘導だと決めつけてしまい、青→赤→緑の順序で切断すると、断頭四角柱、断頭三角柱の計算などに分割して求めることになり、複雑になってしまう。（※計算ミスの可能性も高くなる。）
• 一方、青→緑→赤の順序で切断すると、②は四角すいHーABEF から　四角すいHーUSRT を引いたものになる。（紫）
• こうなると、計算が簡単になる。
• H-ABEF ＝　4 × 5 × 3 × 1/3 = 20 cm³
• 四角すいHーUSRTは、三角すいU-HRT　と、三角すいU-SHRに分けて考える。
• △URHは△SRHに等積変形できる。（USとTRHの面が平行であるため。）
• となると、底面は△RSHで共通と考えられ、高さはそれぞれTRとUSになり、まとめて計算できる。
• U-HRT 、三角形HRTの高さは側面の相似より求める。PT：TR＝AP：HR＝１：２。
• TR＝5 × 2/3 = 10/3 cm
• U-SHR 、三角形SHRの高さは相似より求める。US : QU = SH : BQ = 3 : 2 。
• US = 5 ×3/5 =  3 cm
• △RSH＝△PQD＝12/5 cm²
• HーUSRT = 12/5 × (10/3 + 3) × 1/3 = 12/5 × 19/3 × 1/3 = 76/15 cm³
• ゆえに、② ＝（H-ABEF）ー　（HーUSRT） 20- 76/15 = 224/15 cm³

5.問い続ける。
（出た結論に対して「なぜ？」「だから？」「本当に？」と問い続けて見落としや新たな発見につなげる。）

• 切断面に間違いはないかを再度検証すること。
• 今回は間違いないので、大丈夫。

• DA:DP=3:2
• DB:DQ=5:3
• △DAB - △DPQ ＝(4 × 3 × 1/2 ) - (4 × 3 × 1/2 ) × 2/3 × 3/5 = 6 - 12/5 = 18/5 cm²
• ① = 18/5 × 5 = 18 cm²

• H-ABEF ＝　4 × 5 × 3 × 1/3 = 20 cm³
• 四角すいHーUSRTは、三角すいU-HRT　と、三角すいU-SHRに分けて考える。
• △URHは△SRHに等積変形できる。（USとTRHの面が平行であるため。）
• となると、底面は△RSHで共通と考えられ、高さはそれぞれTRとUSになり、まとめて計算できる。
• U-HRT 、三角形HRTの高さは側面の相似より求める。PT：TR＝AP：HR＝１：２。TR＝5 × 2/3 = 10/3 cm
• U-SHR 、三角形SHRの高さは相似より求める。US : QU = SH : BQ = 3 : 2 。US = 5 ×3/5 =  3 cm
• △RSH＝△PQD＝12/5 cm²
• HーUSRT = 12/5 × (10/3 + 3) × 1/3 = 12/5 × 19/3 × 1/3 = 76/15 cm³
• ゆえに、② ＝（H-ABEF）ー　（HーUSRT） 20- 76/15 = 224/15 cm³

以上

• 紙面上で立体を再現する手順を身につけておく必要がある。
• 縦軸、横軸、高さ軸に分解して考えること。
• 上から見た図で考えること。
• 相似や比を活用すること。
• これらを、丁寧に、正確に積み上げる粘りも必要である。
• 普段から立体を作図する時間を多くすることで、見え方も鍛えられます。