学習の吸収率を定義する(見える化)
「同じ塾で同じクラスなのに成績に差が出ているのは何故?生まれ持った才能の違いなの?先取りの差?」こんな疑問を持ったことはありませんか?
成長に差が出る要因は才能の違いでも先取りの差でもなく、学習の吸収率にあります。
そして、学習の吸収率は「学習方法」と「学習環境」から構成されています。
学習の吸収率 = 学習方法 × 学習環境
これから吸収率を高める学習方法と学習環境について詳しく説明していきたいと思います。
①吸収率を高める「学習方法」とは
ずばり、吸収率を高める学習方法とはクリティカルシンキング(批判的思考)を習得することです。
ビジネスシーンではよく登場するものの中学受験では聞き慣れないクリティカルシンキングですが、これはDeSeCo(デセコ)や新学習指導要領(文部科学省が告示)において、これからの時代に不可欠な「生きる力」の根幹と位置付けられている重要な能力です。2020年を目指していた大学入試改革の行方も不透明ではありますが、目指す方向性は同じです。
沢山の練習問題や入試問題の解き方を覚えるのではなく、問題を通して難問解答の鍵を握るクリティカルシンキングをコツコツと鍛えるのです。
クリティカルシンキングとは?
ここでは中学受験(小学生の学習)における思考法、伸びる学習方法についての視点で解説していきます。
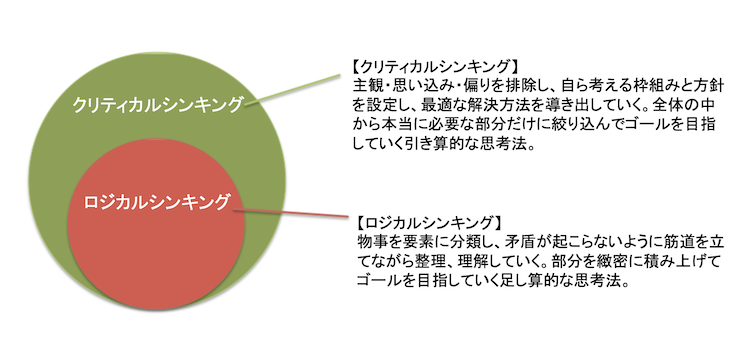
ロジカルシンキング(論理的思考)とは目的に合わせて、物事を要素に分類し、矛盾が起こらないように筋道を立てながら整理、理解していく思考法のことです。情報をモレなく、ダブりなく分類整理し、「なぜ?」と問いかけ原因を探り、「つまり?」と問いかけ結論を探っていきます。
クリティカルシンキング(批判的思考)とは主観・思い込み・偏りを排除し、「本当にこの前提は正しいのか?」「そもそも考えるべきことは何か?」「どんな項目について考えれば答えが出そうか?」という視点を持ち続け、自ら考える枠組みと方針を設定し、複数の可能性の中から最適な解決方法を導き出していく思考法のことです。
部分を緻密に積み上げてゴールを目指していく「足し算的なロジカルシンキング」に対して、全体の中から本当に必要な部分だけに絞り込んでゴールを目指していく「引き算的なクリティカルシンキング」という構図になります。
中学受験においてクリティカルシンキングを習得すべき理由
まずは下記のグラフをご覧ください。
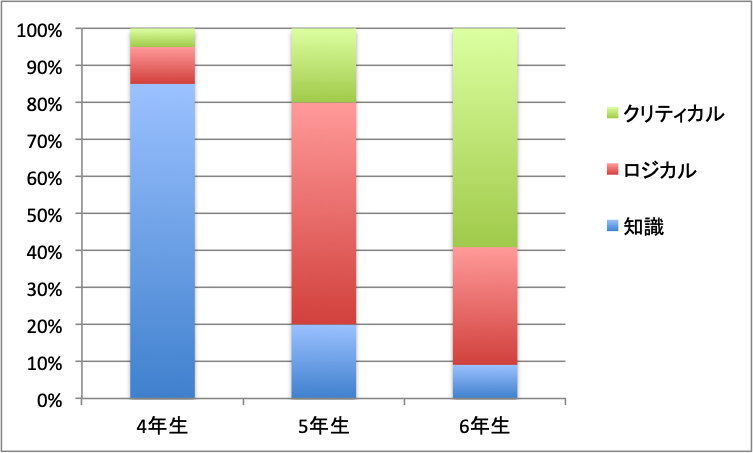
これは公開模試(算数•国語•理科•社会)などにおいて、「どのような能力が必要とされているのか?」を学年ごとに見える化したものです。
4年生→5年生→6年生と進むにつれてクリティカルシンキングの重要性が増していきます。
ロジカルシンキングもクリティカルシンキングもどちらも問題解決の思考法であり、どちらも必要な能力と言えます。しかし、問題がシンプルであればロジカルシンキングが十分に機能するのですが、問題が複雑になってくると不要な情報は削ぎ落とし必要な部分だけを取り出すクリティカルシンキングが欠かせなくなってきます。
ロジカルシンキングという道具(定理や知識)を持って、クリティカルシンキングで未開の地(難問)を切り開いて行くようなイメージを持っていただければと思います。
最難関校ではこういった複雑な問題の出題量が多い傾向があり、合否の差を分ける問題になってくると考えられます。
学習スタイルを変化させよう
続いて、上記の内容を踏まえたうえで、各学年における最適な学習スタイルを表にまとめます。
| 学年 | 構成 | 学習スタイル |
| 4年生 | 知識中心 | 定理、公式、言葉、現象、事実などを暗記していく。 |
| 5年生 | ロジカル中心 | 暗記ではなく、仕組み、つながり、根拠などについて理解と表現を深めていく。論理の基礎を固める。 |
| 6年生 | クリティカル中心 | 類似問題のパターン検索ではなく、着眼点を磨き、論理を自由に使いこなすことを訓練する。問題解決の総合力を高める。 |
このように学年や学習が進むごとに学習スタイルを変化•進化させていくことが必要です。
※変化(適応、進化)させず暗記偏重になりすぎると伸び悩みに陥ってしまう可能性もありますので注意が必要です。
クリティカルシンキングの鍛え方
受験科目に当てはめると、算数では「数」や「図形」などを通して、国語では「言葉」を通して、理科では「現象」を通して、社会では「事実」を通してクリティカルシンキングの能力を問われてきます。
クリティカルシンキングの基本手順
- 目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。) - 前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。) - 目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。) - 構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。) - 問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
※クリティカルシンキングを取り入れた学習手順については各レシピで具体的に解説していきます。
宿題や過去問を解く際にやみくもに解き始めるのではなく、上記のような手順を意識して「『考える枠組み』を自ら考える」という思考のトレーニングを行います。
始めは手間に感じるかもしれませんが、これを継続するとラッキーに頼ることなく、安定的に初見の難問を解くことができるようになってきます。
②吸収率を高める「学習環境」とは
当サイト「のびてく」で言う学習環境とは「家庭•親」のことを指します。(※決して立派な学習机や快適な子供部屋のことを指すのではありません。)
そして、親の役割は「自力で考える時間を十分に確保すること。」と「子供と同じ目線に立つこと。」です。
その理由について説明していきます。
思考時間を十分に確保する
ロジカルシンキングは解説中心の授業を受け、徹底的な復習で解法をパターン暗記することによって鍛えることが可能です。ティーチング中心のファストラーニングと言えます。
一方、クリティカルシンキングはヒントの無い状態から思考に偏りが出ないように俯瞰的に物事を分析し、自力で糸口を探し出す必要があるため、効率的な学習では鍛えることができません。コーチング中心のスローラーニング&ディープラーニングと言えます。(※ただしロジカルがベースになるのでクリティカルだけでは成り立ちません。)
親も我慢しよう
算数一問に対して1時間以上かかっても糸口が見つからないなんてこともザラに出てきます。闇雲に勘に頼って解くのであれば1時間も経たずに考えることがなくなってギブアップするでしょう。しかし、クリティカルな思考で挑戦しているのであれば、仮説検証を何度も何度も繰り返していくので粘れるのです。
親が我慢できずにテキストの解答(解説)を見て「答えに誘導する」のではなく、正しい考え方の手順を踏むように導くようにしましょう。
たった一問に1時間かけてしまった時、もっと沢山の問題を解いた方が良いように感じるかもしれませんが、解説通りに解いても知識が増えるだけでクリティカルな思考は鍛えられません。
また、入試では全く同じ問題が出題されることはまずないので知識は役立ちません。それよりも1時間考えざるを得なかった部分は「自分の苦手な部分」であった訳で、そこに対して確実に鍛錬し成長したはずです。これこそ、正しい学びと言えます。
始めは本当に時間が掛かりますが、見かけの学習効率を追わず、一見無駄にも思える思考時間を十分に確保することが最重要なのです。
子供と同じ目線に立つ
もうひとつ学習環境(家庭)として大事なのが子供と同じ目線に立ち、子供の苦労や頑張りを深く理解してあげることです。
一番良いのは親も一緒に問題を解いてみることです。全問ではなくて結構です。お子さんが行き詰まっている難しそうな問題を一緒に考えてみてください。
解けなくても良いのです。解答(解説)は一切見ずに、子供と同じように「難しいな〜」と悩んでみてください。
テストの不正解に対して「これ解けなくてどうするのよ!」と自分の焦りを子供にぶつけてしまうことも無くなると思います。 (※最も簡単で効果的なアンガーマネジメントです。)
そして心から「頑張ってるね!」偉いね!と褒めてあげることができると思います。
③もっと没頭しよう!もっと寄り道しよう!もっと楽しもう!
学習の吸収率 = 学習方法 × 学習環境
さて、じっくりと学習することでクリティカルシンキングを鍛え、吸収率を高められることをお伝えしてきました。
最後に吸収率の高い状態を維持し、好循環サイクルにもっていくポイントについて説明します。
好きこそ物の上手なれ
子供たちは分かれば勉強が絶対に好きになります。
また、繰り返しになりますがクリティカルシンキングは「分からない問題」に対して思考のフレームを自ら形成することができます。
- 「分からない=やばい」 となりません。
- 「分からない=よし、どこから手をつけようか。必ず解けるぞ!」 となります。
分からない、知らない局面に対峙したとき落ち着いた精神状態を保てる、根底には自信があるというのは、中学入試の本番においてとてつもないアドバンテージになってきます。
また、「分からない、知らない。」という状態からスタートできるので、どんどん挑戦してみたくなってきます。(自信があるから。)
つまり、これは好奇心そのものですので、詰め込まなくてもどんどん没頭していきます。
好奇心はときに寄り道や回り道を好みますが、これは絶対に必要な時間ですので、削らずに確保してあげましょう。
この好奇心がやがては意志へとつながっていきます。
やらされではなく、自らの意志で勉強するとすれば、それは究極的に吸収率の高い状態と言えます。
中学受験は決して平坦な道ではありませんが、子供たちは自ら伸びる力を宿しています。
その力を信じ、伸ばしていってあげましょう!
