今回は2021年度の灘中学校の算数1日目で出題された平面図形の問題です。色々な解き方があります。
問題(2021年度、灘中学校の算数1日目)
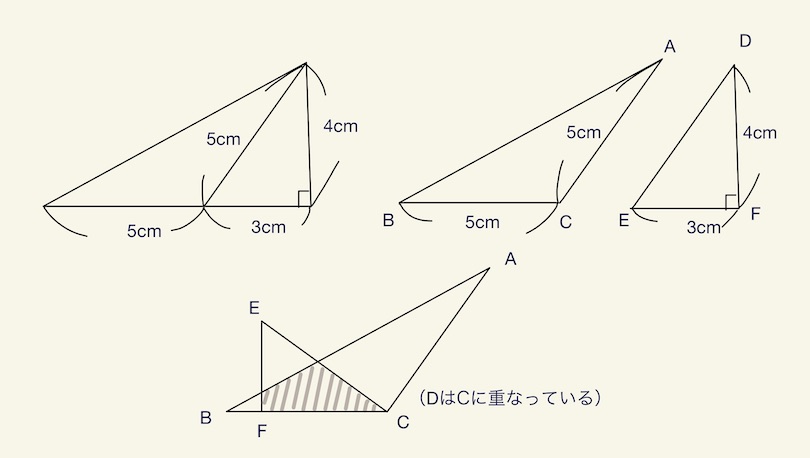
直角三角形を図のように三角形ABCと三角形DEFに切り分けます。これらの2つの三角形を図のように重ねたとき、斜線部の面積は( ア )cm²です。(ア)を求めなさい。
学習noteの進め方
まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。(※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。)
その後(解き終えたら、または目安時間が経過したら)、下にスクロールして解説(思考の例)をじっくり読んでください。
ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ(クリティカルシンキング)を鍛えることが今回の目的です。
クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう!
クリティカルシンキングのトレーニング手順(批判的思考)
- 1
目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)- 2
前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)- 3
目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)- 4
構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)- 5
問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
クリティカルシンキングの例(解説)
1.目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)
- 「斜線部面積の出し方」と「必要な長さがどこか」が見抜けるかどうかを問われているのだな。
- 「必要な長さ」を求める際、今ある条件から「出せる長さ」と「出せない長さ」の見極めをしないとハマってしまうな。
このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。
2.前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)
- 切り取っているので、単純に分かる長さを書き入れる。
- 切り取る前のもとの辺の長さ(形状)も活用する。
ここでは思い込を排除し、事実だけを書き入れて整理することが大切です。
3.目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)

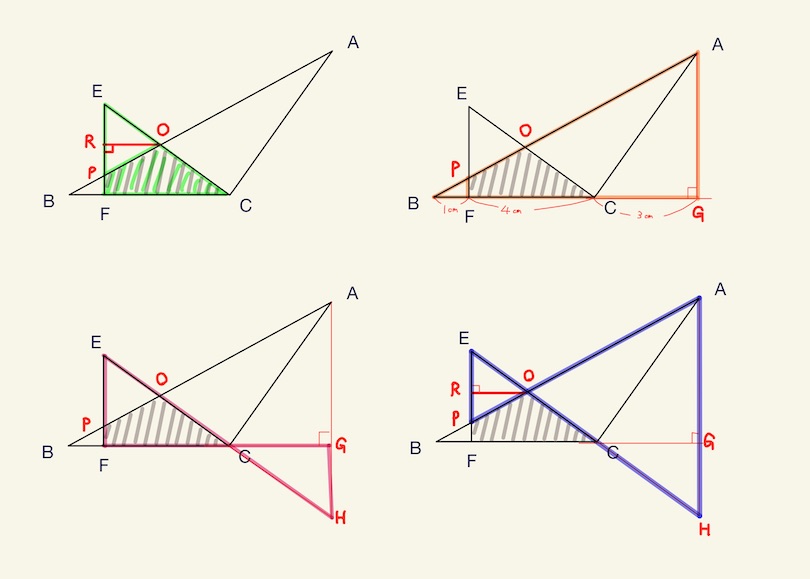
- OQに補助線を入れると、相似形が活用でき、斜線部を左右に2分割して求められそうだ。(まだ決定ではない。)
→OQの長さが欲しい。しかし、FQ(または辺QC)の長さが分からないので、相似を使っても出ない。
- ORに補助線を入れると、△EFCー△EPOで、斜線部を求められそうだ。(まだ決定ではない。)
→ORの長さが欲しい。BFが1cmと分かるので、分割前の△ABGと△PBFの相似よりPFとEPの長さは出る。
→よって、そこから△CEFと△CHGの相似、△OEPと△OHAの相似を使ってORの長さも出せそうだ!(これを方針としよう!)
このように、ここでは2つの方針が見えるが、それぞれの方針の可能性を更に追求し、どちらの方針を優先するかを決めよう。
4.構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)
- △PBFと△ABGの相似より、PF=1/2 cm と分かる。よって、EP=5/2 cm となる。
- 続いて、△CEFと△CHGの相似から、GH=9/4 cm と分かる。
- すると、AH = 4 + 9/4 = 25/4 cm となる。
- ここで、△OEPと△OHAの相似に注目すると、EP:HA = 5/2 : 25/4 = 2 : 5 となる。
- よって、OR=(4+3) × 2/7 = 2cm となる。
- 斜線部の面積は (4 × 3 ÷ 2) – (5/2 × 2 ÷ 2) = 6 – 5/2 = 7/2 (cm²) となる。(以上)
このように、切り取った図形の移動による「分かっている長さ」だけに注目することで、出せる長さと出せない長さを選別することが可能になる。
ここまでが、ロジカル思考を重視した解法である。
5.問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
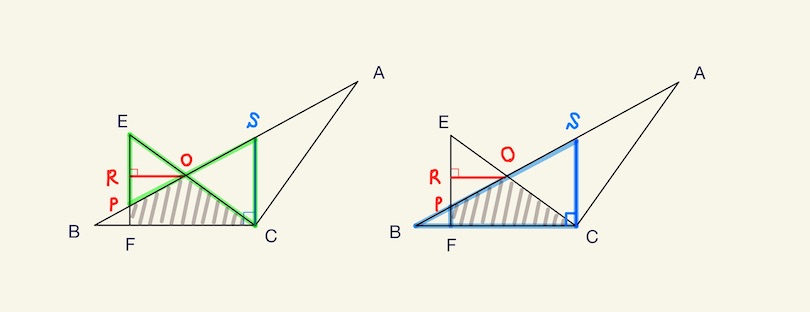
- 相似の基本に立ち返り、1組の長さが分かっている部分に注目して思考する。
- 更に、FC=4cmと分かってもいる。つまり、点Cから真上に補助線を入れるとよいかも!
- 見えた!△OEPと△OCSが相似だ!
- CSは△BSCと△BPFの直角三角形の相似から5/2cmと出る。
- つまり、△OEPと△OCSは1:1の相似(合同)だ!
- となると、OR(高さ)はFC(4cm)の半分なので2cmと分かる。(暗算レベル)
△CEF=3 × 4 ÷ 2 = 6cm²
△OEP=5/2 × 2 ÷ 2 = 5/2cm²
斜線部の面積 = 6 – 5/2 = 7/2 (cm²)
こちらがクリティカル思考による解法であり、よりシンプルに解答することができる。たまたまではなく、分かっている条件から逆算して、狙って補助線を入れることができる。
灘中の1日目などは問題数も多く時間との勝負でもあります。このようにクリティカルな思考を習得することで、短時間かつ高精度で解答することが可能となります。(※灘中の算数は思考には時間をかけ、計算は短時間で済ませるタイプの問題が非常に多いです。)
解答
- 点Cから真上に補助線を入れ、交点をSとする。
- △OEPと△OCSが相似。
- 辺CSは△BSCと△BPFの直角三角形の相似から5/2cmと出る。
- つまり、△OEPと△OCSは1:1の相似(合同)。
- となると、辺OR(高さ)は辺FC(4cm)の半分なので2cmと分かる。
△CEF=3 × 4 ÷ 2 = 6cm²
△OEP=5/2 × 2 ÷ 2 = 5/2cm²
斜線部の面積 = 6 – 5/2 = 7/2 (cm²)
以上。
※他にも相似を使った色々な解き方があるよ。試してみてね。結果的に一番計算が楽なのは上記の解き方かもしれないね。
解答に必要となる前提知識
- 必要な前提知識
- 難易度
- 分数の計算
- ★☆☆☆☆
- 比
- ★☆☆☆☆
- 三角形の面積
- ★☆☆☆☆
- 相似形
- ★★☆☆☆
この問題から学んだこと
- 相似を目的に平行な補助線を入れるには、長さが具体的に分かっている「点」に対して入れないと使えない。
- なるべくシンプルに、手数少なく済むように相似を活用する意識を持つと良い。
- どことどこを比較しているのかを客観的かつ明確にすること。