今回は2018年度の灘中学校の算数1日目で出題された平面図形、光の反射の問題です。与えられた条件が少ないので、逆にこの条件だけでできることに絞り込むことが大切。極めてシンプルな条件で解かせる灘中らしい問題のひとつ。難しく考えすぎるとハマって超難問に感じてしまうこともあるので、冷静にやれる事だけに集中しましょう!
問題(2018年度、灘中学校の算数1日目)

光が鏡で反射するときには、図1のように角アと角イの大きさが等しくなります。
図2は、3枚の鏡AB、BC、CAで、何回も反射しながら同じ経路を繰り返し進む光の様子を表しています。
このとき、角ウの大きさは( )度です。
学習noteの進め方
まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。(※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。)
その後(解き終えたら、または目安時間が経過したら)、下にスクロールして解説(思考の例)をじっくり読んでください。
ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ(クリティカルシンキング)を鍛えることが今回の目的です。
クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう!
クリティカルシンキングのトレーニング手順(批判的思考)
- 1
目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)- 2
前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)- 3
目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)- 4
構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)- 5
問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
クリティカルシンキングの例(解説)
1.目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)
- 「光の反射」、「同じ経路を繰り返したどる」ということに、何か意味はあるのか?
- 可能性として、ア=イ で式を結びつけることを使うのかもしれない。(まだ根拠がなく、わからないが。)
このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。
2.前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)
- 104度,37度,39度の三角形なので、おそらく正三角形、直角三角形などの特殊な形になるという意味ではないだろう。
- となると、補助線を入れて図形を作っていくアプローチは通じないだろう。
- となると、残るは「図1のア=イ」の性質を上手く活用して、徐々に出していくしかないだろう。
ここでは思い込を排除し、事実だけを整理することが大切です。
3.目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)
- 一般的な知識より、とある一つの角を2通りに表現できれば、角度を求められるだろう。はたして今回は使えるのか?
- 何か見落としはないだろうか?
- そうか、「図1のア=イ」の光の反射の性質は2通りの表現につながるんだな!
- あとは三角形の内角の和が180度、三角形の外角定理の基本を使って、表現していこう。
- もう何か見落としはないだろうか?
- あ!一つ一つの角度は出せなくても、2つの合計(ペア)は表現できるので、ペアで攻めていけば良いのかも!?
ここでは方針の検討をしっかり行います。
4.構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)
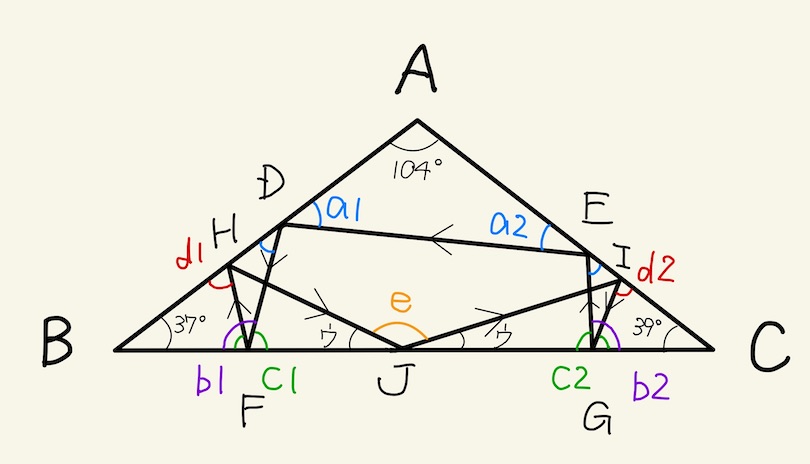
- 上の図のように、a = a1 + a2, b = b1 + b2, c = c1 + c2, d = d1 + d2 とおく。
- △ADEの内角の和より、a=180-104=76 とわかる。
- 光の性質より、角BDF+角CEG = 76 である。
- よって、△BDFと△CEGを合わせて(ペア)で考えると b=(180×2) – (76+37+39) = 208 とわかる。
- 一方、c=(180×2) – b = 360 – 208 = 152 とわかる。
- また、光の性質より、角HFB+角IGC = c =152 である。
- △BHF+△CIGを合わせて考えると、d = (180×2) – (37+39+152) = 132 とわかる。
- 光の性質より、角AHJ+角AIJ = d =132 である。
- 四角形AHJIの内角の和360度で考えると、e = 360 – (104 + 132) = 124 とわかる。
- よって、角ウ=(180 – 124) ÷ 2 = 28度
以上。
5.問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
- 三角形の角度が変わっても内角の和は変わらないので、合計(ぺア、セット)で考えること。
- 光の性質から、置き換えができること。
- この二つをシンプルに理解していれば、切り口が見えるんだな。それを問われているのだろうな。
解答
上記の解説より、
- 上の図のように、a = a1 + a2, b = b1 + b2, c = c1 + c2, d = d1 + d2 とおく。
- △ADEの内角の和より、a=180-104=76 とわかる。
- 光の性質より、角BDF+角CEG = 76 である。
- よって、△BDFと△CEGを合わせて(ペア)で考えると b=(180×2) – (76+37+39) = 208 とわかる。
- 一方、c=(180×2) – b = 360 – 208 = 152 とわかる。
- また、光の性質より、角HFB+角IGC = c =152 である。
- △BHF+△CIGを合わせて考えると、d = (180×2) – (37+39+152) = 132 とわかる。
- 光の性質より、角AHJ+角AIJ = d =132 である。
- 四角形AHJIの内角の和360度で考えると、e = 360 – (104 + 132) = 124 とわかる。
- よって、角ウ=(180 – 124) ÷ 2 = 28度
以上。
解答に必要となる前提知識
- 必要な前提知識
- 難易度
- 三角形の内角の和
- ★☆☆☆☆
- 三角形の外角定理
- ★☆☆☆☆
この問題から学んだこと
- 初見でも、消去的に「補助線をいれてどうにかなることはない」とこの捨てられれば、ハマることはない。
- 現実的にできることが限られているので、あせらず、その条件のみで解けると思うことで道が開ける。
