今回は2018年度の灘中学校の算数1日目で出題された平面図形の問題です。極めてシンプルな問いですが、与えられた条件の意味を深く考えることでアプローチ方法が見えてきます。クリティカルシンキングが求められる灘中らしい問題のひとつです。楽しんで解いてみてね。
問題(2018年度、灘中学校の算数1日目)
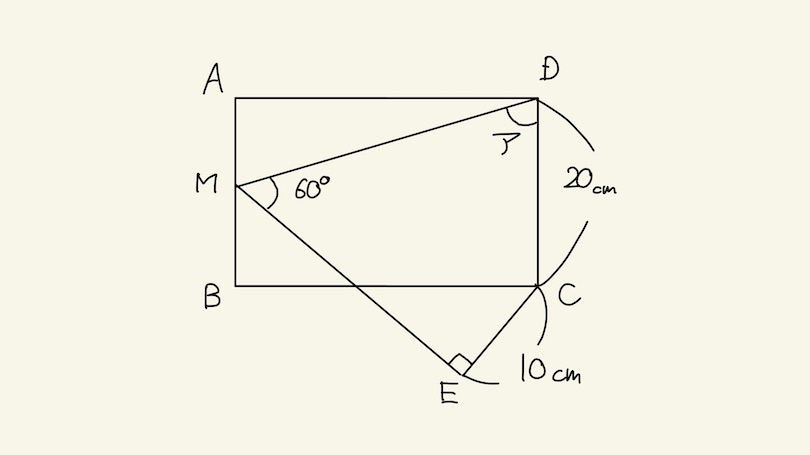
右の図で、四角形ABCDは長方形で、辺ABの真ん中の点がMです。また2本の直線CE、MEは直角です。
この時、角アの大きさは( )度です。
学習noteの進め方
まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。(※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。)
その後(解き終えたら、または目安時間が経過したら)、下にスクロールして解説(思考の例)をじっくり読んでください。
ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ(クリティカルシンキング)を鍛えることが今回の目的です。
クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう!
クリティカルシンキングのトレーニング手順(批判的思考)
- 1
目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)- 2
前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)- 3
目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)- 4
構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)- 5
問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
クリティカルシンキングの例(解説)
1.目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)
- 極めてシンプルな図形であり、与えられた条件が少ない。
このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。
2.前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)
- 具体的に数値が出るのは「正三角形の60度」、「正三角形の半分にした30度」、「直角二等辺三角形の45度」くらいしかないが、今回は使えなさそう。
- 角度、長さ、一つ一つの意味をしっかり考えよう。
ここでは思い込を排除し、事実だけを書き入れて整理することが大切です。
3.目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)
- やみくもに補助線を入れてはだめ。
- おそらく、角アは90度ー角ADMで出すしかないような気がする。
- 「Mが真ん中(半分)」、「CEとMEは直角」、「CEはCDの半分」、この3つの条件の意味を考えよう。
ここでは考える方向性だけに集中しましょう。
4.構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)
- CEが10cmということは、CDの20cmの半分である。これに意味があるはず。考えると・・・。
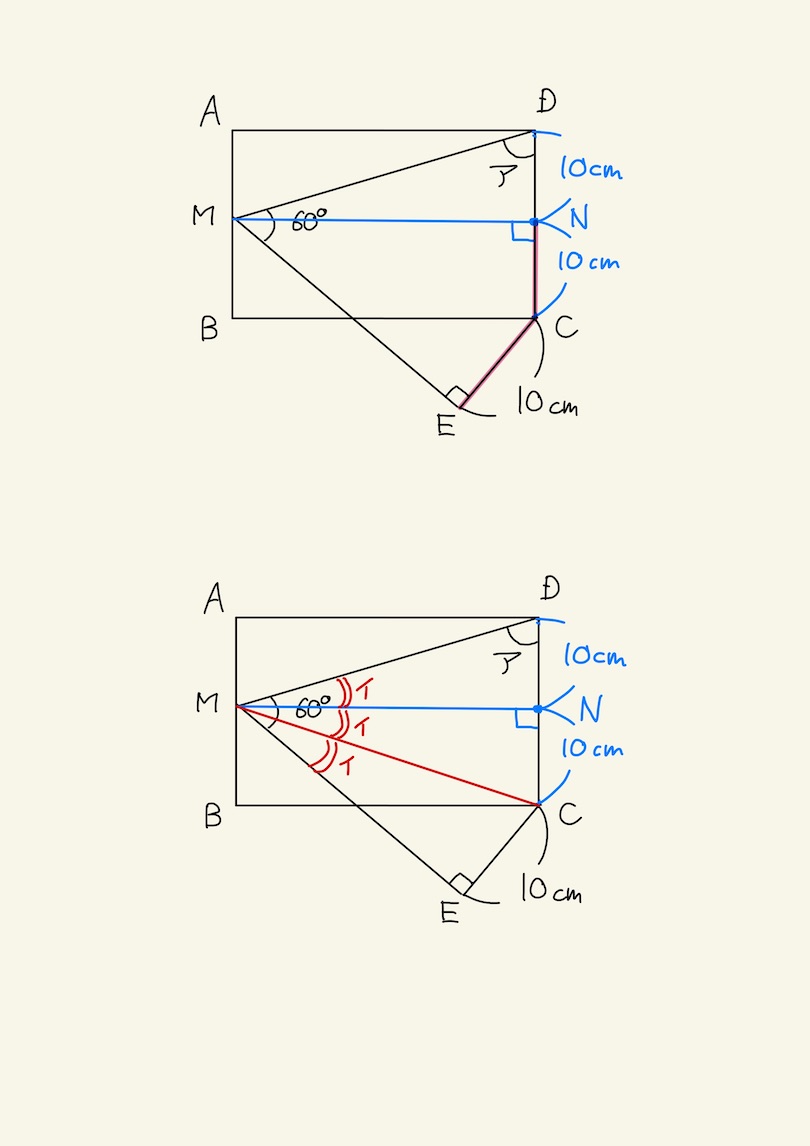
- Mも真ん中(半分)ということは、AM=BM=10cmである。
- CDの中間点をNとすれば、MNとCDは直角になり、CN=DN=10cmとなる。
- 辺ADと辺MNは平行になる!よって、角ADM=角NMDとなる。
- この補助線で、角DME60度 = 角NMD+角NME となる。
- 角NMEが分かればアは出るが。
- あ!MCの補助線を入れると、△MCNと△MCEと△MDNの合同が見えた!(直角三角形の合同条件。)
- 角イ=60÷3 = 20度と分かる。
- よって、ア = 90 – 20 = 70度
5.問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
- 分かってしまえば極めてシンプルだから間違いない。
解答
【別解】
仮に、「おそらく、角アは90度ー角ADMで出すしかないような気がする。」この視点がないとすると
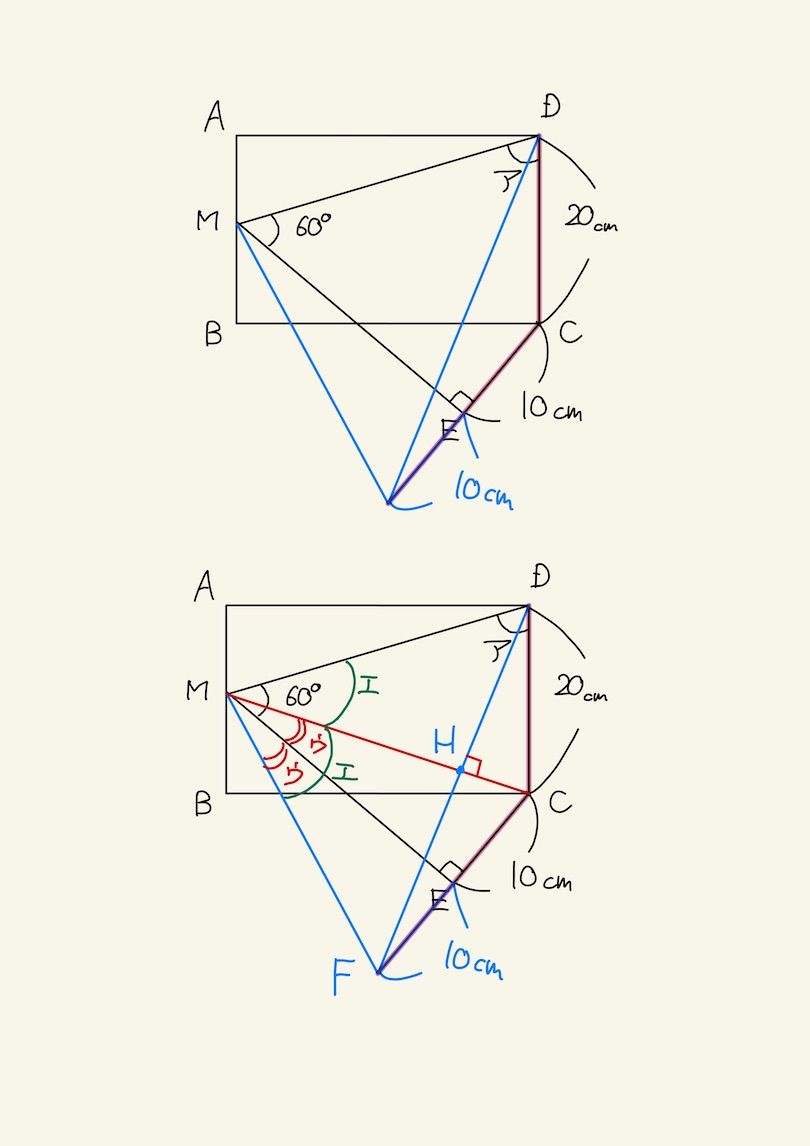
- CE10cmが「20cm半分かつ直角」という点に注目すれば以下のような補助線が思いつく。
- 角ウ=20度と分かり、角DMF=80度となり、角MFH=角MDH = (180-80)÷2 = 50度と分かる。
- 角HFC=角HDC20度(合同)と分かる。
- よって、角ア=50 + 20 = 70度
このように、少し遠回りだが、多少条件を見落としても、粘り強く条件の意味を考えることで正解にたどり着くことができる。
入試本番では緊張から条件を見落としてしまうことが十分に考えられる。多少遠回りしても、大きな方針がずれていなければ正答できるということを覚えておいて欲しい。
以上。
解答に必要となる前提知識
- 必要な前提知識
- 難易度
- 三角形の合同
- ★☆☆☆☆
この問題から学んだこと
- 二等辺三角形と直角の関係(2分割する中間点になる。)
- 三角形の合同条件(直角三角形の合同条件。二つの辺と直角。)
クリティカルに、ロジカルに思考していけば、あっと言う間に正解にたどり着くのだが、やみくもに手をつけてしまうと糸口が見えなくなってしまういます。
上記の手順を参考にして、思考の根拠、思考の流れを学んで欲しい良問です。
難しい問題ではありませんんが、しっかりとクリティカルシンキングが鍛えられます。
誰でも知っていることを、深く理解しているか、複数の視点で捉えられているか、しっかりと応用できるかどうかの問いでしたね。
