速さの問題（灘中）[S-0008-R]

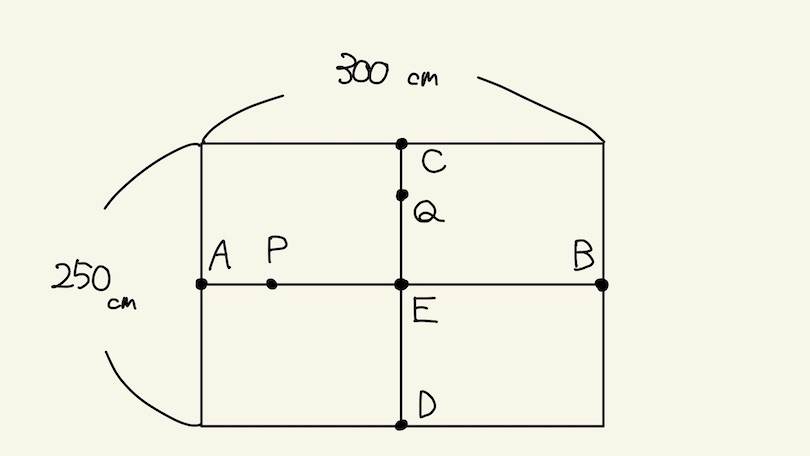
上の図のように、縦250cm、横300cmの長方形があり、各辺の真ん中の点をそれぞれA,D,B,Cとします。また、直線ABと直線CDは点Eで交わります。

点Pは直線AB上にあり、AとBの間を繰り返し往復します。はじめ、PはAを終発して秒速120cmで進み、BまたはAで折り返すごとに速さが0.5倍になります。また、点QはCを出発して一定の速さで直線CD上を進み、Dに着くととそこで止まります。

PとQが同時に出発したところ、ある時刻に同時にEを通りました。このようなQの速さの中で２番目に速いものは秒速（　　　ア　　　）cm、６番目に速いものは秒速（　　　イ　　　）cmです。

（ア）と（イ）を求めなさい。

まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。（※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。）

その後（解き終えたら、または目安時間が経過したら）、下にスクロールして解説（思考の例）をじっくり読んでください。

ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ（クリティカルシンキング）を鍛えることが今回の目的です。

クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう！

1.目的は何かを常に意識する。
（何を問われているのか？どんな理解を試されているのか？など題意を見抜く。）

• 特に複雑な動きや条件は無さそうだ。
• 点Pと点Qの動きを正確に理解するように集中しよう。

このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。

2.前提条件、置かれた環境に合わせて考える。
（思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。）

• 点Pは往復するごとに速さが0.5倍になる。
• 点PがEを通るには1回目だけは秒速120cmと一定だが、2回目以降は往路と復路で速さが異なる。
• 点Qは往復しない。

ここでは思い込を排除し、事実だけを書き入れて整理することが大切です。

3.目的を踏まえたうえで、「考える枠組み」を考える。
（どんな項目について考えればゴールに到着するかの見当をつける。）

• 点Qは往復せず、２番目と６番目の速さを聞かれているだけなので、単純に書き出して整理していくのが一番簡単かつ確実だろう。
• 書き出しながら、整理してみよう。

4.構造的にアプローチする。
（抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。）

• 点PがEを1回目に通過する時をE1とする。以降も同様にE2〜E６とする。
• E1：　往路　150cm÷120cm＝5/4秒　のみ
• E2：　往路　150cm÷120cm = 5/4秒、　復路　150cm÷60cm = 5/2秒、　合計15/4秒
• E3：　往路　150cm÷60cm = 5/2秒、　復路　150cm÷30cm = 5秒、　合計15/2秒
• E4：　往路　150cm÷30cm = 5秒、　復路　150cm÷15cm = 10秒、　合計15秒
• E5：　往路　150cm÷15cm = 10秒、　復路　150cm÷15/2cm = 20秒、　合計30秒
• E6：　往路　150cm÷15/2cm = 20秒、　復路　150cm÷15/4cm = 40秒、　合計60秒

このように、Eを通過するごとに2倍の秒数がかかることが分かる。

（※簡単な時間が2倍になっていく規則が見つかれば、一つ一つを計算する必要もなくなる。）

（ア）は合計5/4 + 15/4 = 5秒

同様に（イ）は合計235/2秒

5.問い続ける。
（出た結論に対して「なぜ？」「だから？」「本当に？」と問い続けて見落としや新たな発見につなげる。）

• 点Qは往復せず、点Dで止まる。
• よって、２番目はE2、６番目はE６の時間から点Qの速さを求めればよい。
• 特に見落としもないので、これでOK！

上記の解説より、

（ア）125cm ÷ 5秒 = 毎秒25cm

（イ）125cm ÷ 235/2秒 = 毎秒50/47

以上。

• 問題文から動きを正確に把握する。
• 点Qが往復しないという点に注目すれば（見落とさなければ）現実的に書き出して整理することが一番楽である。