今回は2016年立命館守山中の算数図形の問題です。頻出の基本的な問題ですが、色々な解法が設定されている良問です。ただ解くだけでなく、アプローチの根拠をどこに持つかにこだわり、思考力を鍛えましょう。中高一貫や有名校はもちろん、最難関を目指す5年生などにもしっかりと理解して欲しい問題です。
問題
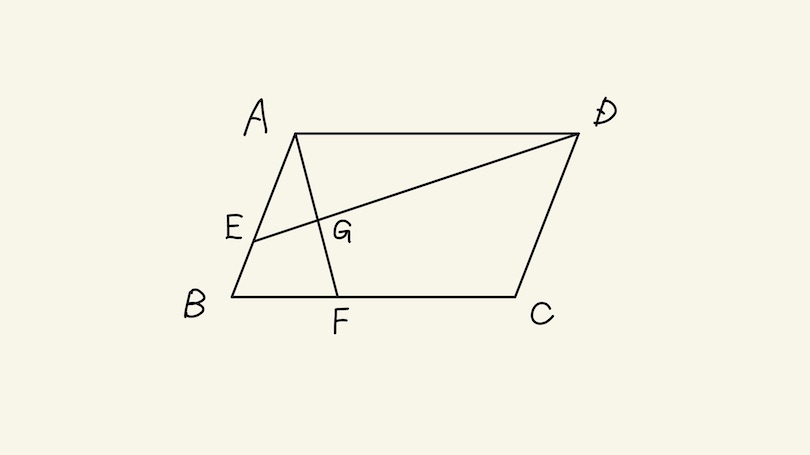
上の図の平行四辺形において、AE:EB=3:2、BF:FC=1:2です。
(1)三角形ABFと平行四辺形ABCDの面積比を求めなさい。 ( : )
(2)三角形AGDと四角形EBFGの面積の比を求めなさい。( : )
学習noteの進め方
まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。(※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。)
その後(解き終えたら、または目安時間が経過したら)、下にスクロールして解説(思考の例)をじっくり読んでください。
ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ(クリティカルシンキング)を鍛えることが今回の目的です。
クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう!
クリティカルシンキングのトレーニング手順(批判的思考)
- 1
目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)- 2
前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)- 3
目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)- 4
構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)- 5
問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
クリティカルシンキングの例(解説)
1.目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)
- 問い(1)に関しては問題ない。
- 問い(2)に関しては比と相似を上手く使って求めるのだろう。
- どこに相似が隠れていて、どう活用するのが一番簡単かを考えることにしよう。
このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。
2.前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)
- ベースが平行四辺形だから、相似、等積変形の三角形などが活用できる。
- 四角形EBFGの面積をどのように求めるかがポイントだな。
ここでは思い込を排除し、事実だけを書き入れて整理することが大切です。
3.目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)
- 三角形AGDの面積を求めるにはEG:GDが分かると良さそうだな。
- 四角形EBFGをどう分割するかを考えよう。
→(ア)EFに補助線を入れて分割(斜めに)する場合。
→(イ)BGに補助線を入れて分割(斜めに)する場合。
→(ウ)EからBCに平行な補助線を入れて(上下に)分割する場合。
→(エ)GからABに平行な補助線を入れて(左右に)分割する場合。 - ア〜エ、考えられる4種類のそれぞれの分割方法の先をイメージして方針を決定しよう。
このように、まずは考えられるパターンを洗い出し、その後に冷静に方針決定する方がハマらなくて良い。
4.構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)
- 「EG:GDが分かると良さそう」 これがア〜エの方針決定の根拠になる!
(※ EBFGにもAGDにも一石二鳥で使えるのが理想である。)
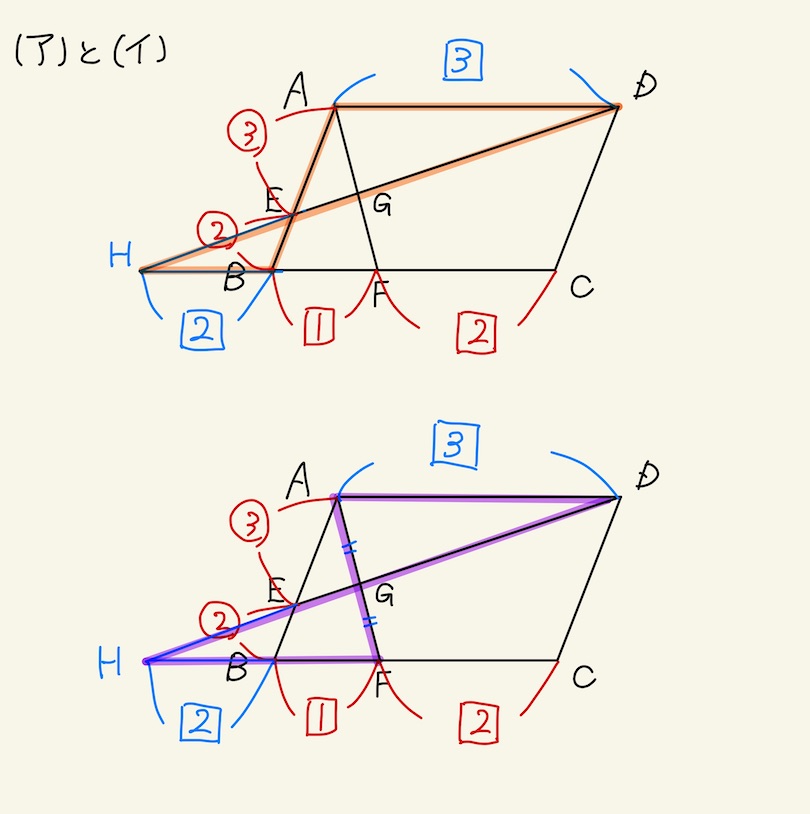
(※ EG:GDが出ないなら、AGD=AEDーAEG から求めることになるだろう。) - (ア)の場合、EG:GDは出ない。
(※GEを延長した線とCBの延長した線の交点をHとすると、△GADと△GFHが相似となり、AG:GF=1:1と出る。)
(※△AGD=△AEDー△AEGから出せる。) - (イ)の場合、EG:GDは出ない。
(※GEを延長した線とCBの延長した線の交点をHとすると、△GADと△GFHが相似となり、AG:GF=1:1と出る。)
(※△AGD=△AEDー△AEGから出せる。)
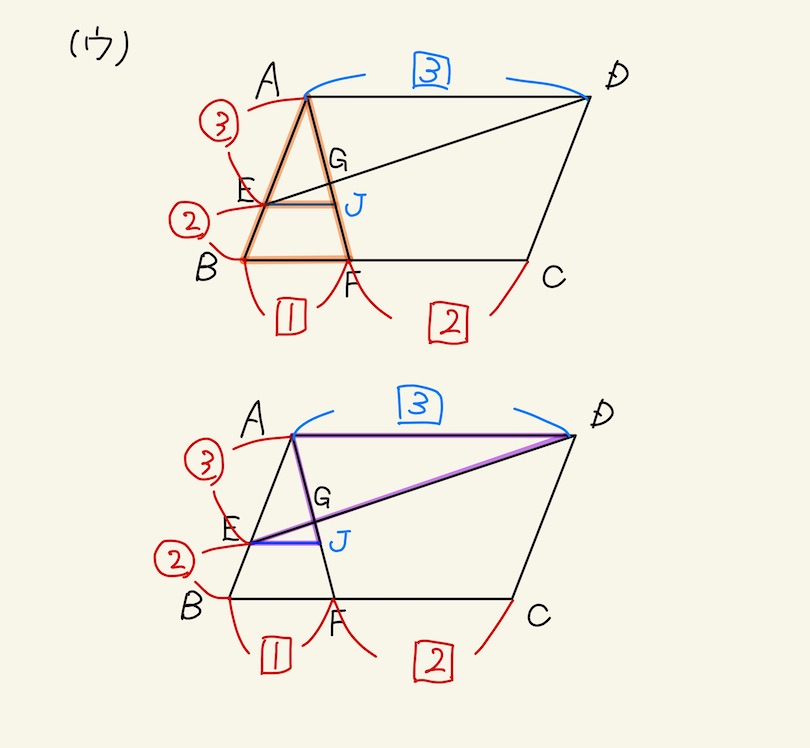
- (ウ)の場合、EG:GDが分かる!
(※△ABFと△AEJが5:3の相似。) - (エ)の場合、何も分からない。
5.問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
- (ア)(イ)の方針でも出せるが、(ウ)の場合が最も計算も少なくシンプルに求められるので、(ウ)の方針で間違いない!
解答
(1)三角形ABFと平行四辺形ABCDの面積比を求めなさい。 ( : )
△ABF=1/2 × 1/3 =1/6
ゆえに、1:6
(2)三角形AGDと四角形EBFGの面積の比を求めなさい。( : )
(ウ)の方針と上記の図より、
- 相似より、BF:EJ=5:3
- EJ=3/5
- 相似より、EJ:DA=3/5:3=1:5 = GE:GD
- △AGD=1/2 × 3/5 × 5/6 = 1/4
- □EBFG=△ABFー△AEG=1/6 ー(1/2 × 3/5 × 1/6)=7/60
- △AGD:□EBFG = 1/4 :7/60 = 15:7
以上。
解答に必要となる前提知識
- 必要な前提知識
- 難易度
- 面積比
- ★☆☆☆☆
- 相似
- ★☆☆☆☆
この問題から学んだこと
- 根拠に基づき必要な部分を絞り込み、今わかっている条件を最大限かつシンプルに活用する。
- 分数の計算を楽にするために、平行四辺形の面積を便宜的に「60」などとしても良い。
