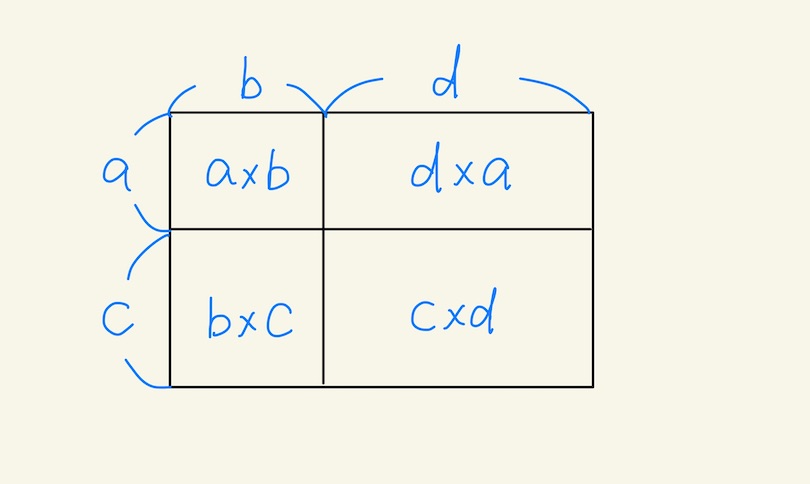数論（灘中）[S-0004-C]

４個の整数a,b,c,dがあり、bはaより1大きく、cはbより1大きく、dはcより1大きいです。

a×b+b×c+c×d+d×aを計算すると2400になるとき、aは（　　ア　　）です。

（　　ア　　）を求めなさい。

まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。（※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。）

その後（解き終えたら、または目安時間が経過したら）、下にスクロールして解説（思考の例）をじっくり読んでください。

ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ（クリティカルシンキング）を鍛えることが今回の目的です。

クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう！

1.目的は何かを常に意識する。
（何を問われているのか？どんな理解を試されているのか？など題意を見抜く。）

• a,b,c,dの4つの数から2つを選んで掛け合わせる。そして合計するということの構造的な意味は何か？
• a,b,c,dの4つの関係が1ずつ大きくなり、最終合計が2400であるので、どう上手く絞り込めるか。

このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。

2.前提条件、置かれた環境に合わせて考える。
（思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。）

• 「2つの項目をかける」という行為は「単位×数量」、「濃度×全量」、「縦×横の面積」などがある。
• a,b,c,dから2つを選択して掛け合わせる。組み合わせ方に注目すると、それぞれが2回ずつ使用されている。
• 組み合わせ方に更に注目すると、a,cのグループとb,dのグループに別れることが分かる。
• 1ずつ大きい、合計が2400になるという数値については後に置いておき、先ずは「2つをかける」「合計する」の構造的意味にだけ集中する。

ここでは思い込を排除し、事実だけを書き入れて整理することが大切です。

3.目的を踏まえたうえで、「考える枠組み」を考える。
（どんな項目について考えればゴールに到着するかの見当をつける。）

• a,b,c,d自体に濃度や速さなどの意味は持たされていないので、単純に面積として表現してみる。
• あ！きれいに並べられる。単純に長方形の面積として構造的な意味を持たせて表現できる！
• それぞれ2回ずつ使用するペアリングの意味は「縦」と「横」だったんだ。
• この方向に答えがあるはず！（方針決定）

このように、「掛け合わせることの構造的な意味」と「2400になる数値の絞り込み」を独立させて考えることで、方針決定がスムーズになる。

4.構造的にアプローチする。
（抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。）

• 上記の面積の図より、a×b+b×c+c×d+d×a は (a+c)×(b+d)と言い換えることができる。
• (a+c)×(b+d) = (a+a+2)×(a+1+a+2) = (2a+2)×(2a+4)
• (2a+2)をAとおくと、(2a+2)×(2a+4) = A×(A+2) = 2400 となる。
• 2つの数（差が2）の積が2400になるので、絞り込みのためのあたりをつけると、50×50 = 2500 がある。
• 2400は偶数なのでA×(A+2)は偶数×偶数と分かる。
• 試しに、48×50 = 2400 となり、該当するものがみつかった。
• ゆえにA=2a+2=48なので、a=23 となる。

5.問い続ける。
（出た結論に対して「なぜ？」「だから？」「本当に？」と問い続けて見落としや新たな発見につなげる。）

• 50×50 = 2500からすぐに48が見つかったが、本当に他に答えはないのか？念の為検証が必要。
• 2400を素因数分解すると以下のようになる。
  2400 = 2×2×2×2×2×3×5×5
• Aに5が2つとも入る場合、AとA+2に5が１つずつ入る場合、A+2に5が2つとも入る場合の3パターンが考えられるが、Aも(A+2)もどちらも偶数なので、必ず2が1つは含まれることになる。
• よって、最低でもAかA+2のどちらか一方は10の倍数（2×5）であることが分かる。
• なので50は確定で、48も確定と言える。

• 上記の面積の図より、a×b+b×c+c×d+d×a は (a+c)×(b+d)と言い換えることができる。
• (a+c)×(b+d) = (a+a+2)×(a+1+a+2) = (2a+2)×(2a+4)
• (2a+2)をAとおくと、(2a+2)×(2a+4) = A×(A+2) = 2400 となる。
• 2つの数（差が2）の積が2400になるので、絞り込みのためのあたりをつけると、50×50 = 2500 がある。
• 2400は偶数なのでA×(A+2)は偶数×偶数と分かる。
• 2400を素因数分解すると以下のようになる。
  2400 = 2×2×2×2×2×3×5×5
• Aに5が2つとも入る場合、AとA+2に5が１つずつ入る場合、A+2に5が2つとも入る場合の3パターンが考えられるが、Aも(A+2)もどちらも偶数なので、必ず2が1つは含まれることになる。
• よって、最低でもAかA+2のどちらか一方は10の倍数（2×5）であることが分かる。
• なので50は確定で、48も確定と言える。
• ゆえにA=2a+2=48なので、a=23 となる。

以上。

• 構造的な理解と、数値的な絞り込みを分離して考えることが大切。
• ２つを掛け合わせる（積）意味を冷静に考える。
• 掛け合わせ方（ペア）にも意味があるので、しっかり考えること。
• 頭で考えて分からないときは、事実として図にしてみること。
• 数値の絞り込みには思い込まず、根拠を持ちながら行うこと。