今回は東大寺学園中の算数で出題された円柱を用いた立体と平面の関係性の問題です。
問題(東大寺学園中学の算数)
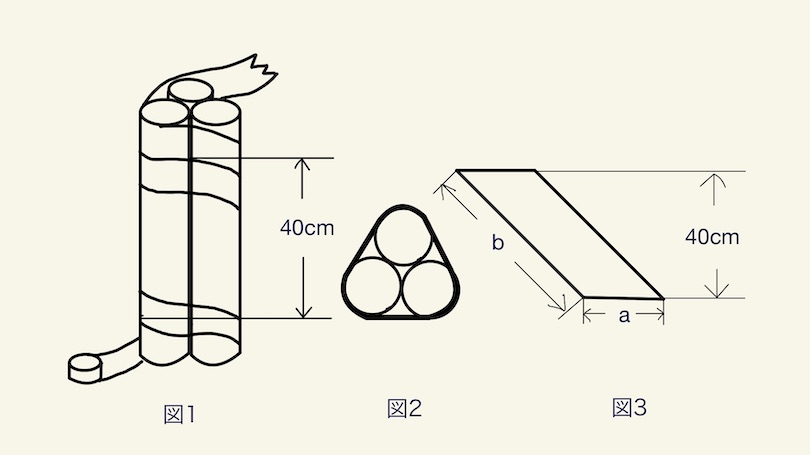
図1のように、直径3cmの円柱の棒を3本まとめて、はば5cmのテープですき間なく重ならないように十分に巻きつけたまま、40cmの長さで棒を切りました。以下の問いに答えなさい。
(1) 切り口の周囲(図2の太線)の長さを求めなさい。
(2) 切り取った部分のテープをはがして伸ばした図3の a , b の長さを求めさなさい。
学習noteの進め方
まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。(※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。)
その後(解き終えたら、または目安時間が経過したら)、下にスクロールして解説(思考の例)をじっくり読んでください。
ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ(クリティカルシンキング)を鍛えることが今回の目的です。
クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう!
クリティカルシンキングのトレーニング手順(批判的思考)
- 1
目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)- 2
前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)- 3
目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)- 4
構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)- 5
問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
クリティカルシンキングの例(解説)
1.目的は何かを常に意識する。
(何を問われているのか?どんな理解を試されているのか?など題意を見抜く。)
- これは「すき間なく巻きつける」ということの理解を試されているのだな。
- 立体を平面に変換して考えなさいという問いだな。
2.前提条件、置かれた環境に合わせて考える。
(思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。)
- 「すき間なく重ならないように巻きつける。」にはテープを斜めに巻きつけるのだな。
- テープの幅にどんな意味があるのか注意しよう。
- 1つの円柱じゃなく、3つの円柱であることの意味にも注意しよう。
- 最後にカット(40cm)されていることにも注意しよう。
3.目的を踏まえたうえで、「考える枠組み」を考える。
(どんな項目について考えればゴールに到着するかの見当をつける。)
- すき間なく巻きついているのだから表面積と平面図形(展開図形)の関係に注目しよう。
- 展開図の特徴させ分かれば解けそうだな。
4.構造的にアプローチする。
(抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。)
(1)
- 「巻きつく」のは一番出っ張った部分に対してである。
- 円とは中心点から等しい長さ(半径)の点の集合である。
- 直線部分と曲線部分に分けて考えよう。
(2)
- 展開図(平面)と立体の関係を正しく分析しよう。
- なるほど、aが周囲の長さになるんだ!
- 高さが40cmと分かっているので側面積からbも分かる!
5.問い続ける。
(出た結論に対して「なぜ?」「だから?」「本当に?」と問い続けて見落としや新たな発見につなげる。)
- 特にひねりやひっかけも無いな。
- 巻きつく理屈に矛盾がなければOKだ。(矛盾なしなのでOK。)
解答
(1)
直線部分は 3 × 3 = 9cm
曲線部分は (3 × π × 120°/360°) × 3 = 3 × 3.14 = 9.42cm
9+9.42 = 18.42cm
(2)
側面の面積は 18.42 × 40 cm²
展開した平面図形(平行四辺形)の面積
a = (1)の周囲の長さと同じなので18.42cm
b = 18.42 × 40 ÷ 5 = 147.36 cm²
※18.42 × 40を計算せず式で残しておくと、最後に計算が楽になるよ。
解答に必要となる前提知識
- 必要な前提知識
- 難易度
- 円周・円弧の長さ
- ★☆☆☆☆
- 四角形・平行四辺形の面積
- ★☆☆☆☆
この問題から学んだこと
- 円柱における最短距離(直線)と平面の関係。
- 巻きつけたものを切り取って広げる。
- 立体から平面へと見た形は変わるが、その中身は変わるはずがない。
- となると、周囲の長さなり、高さなり、面積は変わるるはずがない。
- あとは、どのように巻きついているのかを、冷静に考えるだけでよい。
