場合の数の問題（灘中）[S-0012-C]

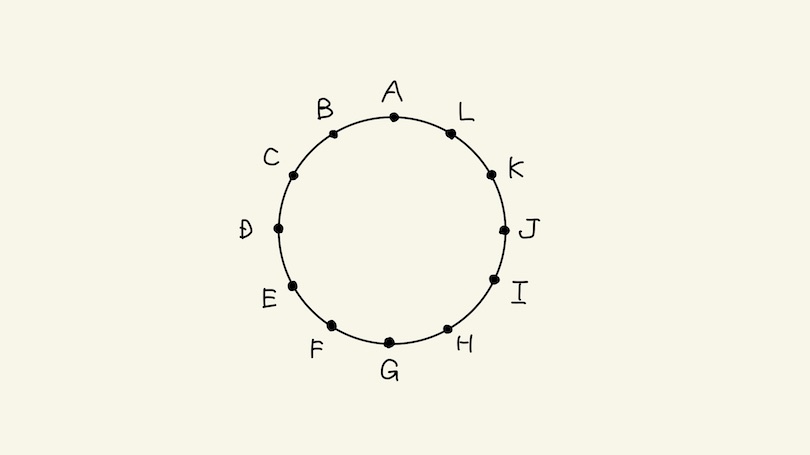
上の図で、円周を12等分した点をA,B,…,Lとします。これら12個の点から異なる3点を選んで三角形をつくるとき、どの辺の長さも円の半径より大きくなるような三角形は全部で（　　　　　）個あります。ただし、合同な三角形でも、頂点が異なるときには異なる三角形として数えます。

まずは目安時間の間、「クリティカルシンキングのトレーニング手順」に沿って考えてください。慣れないかもしれませんが、いつも通りには解かず、必ず思考の手順を守ってください。（※時間に余裕があれば目安時間で区切らず、1時間程度考え続けてもOKです。ただし、完全にお手上げ状態で何も思いつかないのであれば無闇に延長せず、そこで切り上げてください。）

その後（解き終えたら、または目安時間が経過したら）、下にスクロールして解説（思考の例）をじっくり読んでください。

ここでは正解か不正解かが重要なのではなく、問題文をどのように紐解いていくかの目の付けどころと思考の道順が重要であって、そこ（クリティカルシンキング）を鍛えることが今回の目的です。

クリティカルシンキングを習得すれば初見の難問に対応できるようになります。頑張りましょう！

1.目的は何かを常に意識する。
（何を問われているのか？どんな理解を試されているのか？など題意を見抜く。）

• 12個の点の選び方の規則をどうみつけるかの問題だな。

このように、いきなり解き始めるのではなく、まずは客観的に題意の理解に集中することが大切です。

2.前提条件、置かれた環境に合わせて考える。
（思い込みや思考の偏りを排除し、客観的に情報を整理•分析する。）

• 円周上にA〜Lの12個の点がある。
• 点と点の「間隔」も12個ある。
• 「半径より大きくなるように」の部分を、具体的に定義しよう。
• 「合同な三角形でも、頂点が異なる時は異なる三角形として数えます」の部分を、モレ、ダブりがないように注意しよう。

ここでは思い込を排除し、事実だけを書き入れて整理することが大切です。

3.目的を踏まえたうえで、「考える枠組み」を考える。
（どんな項目について考えればゴールに到着するかの見当をつける。）

• 「半径より大きくなるように」ということは、三角形の頂点の間に2つ以上の点がある状態。（※正三角形の一辺が半径と等しいので。）
• A〜Lの「点自体」に注目して考えるのか、それとも点と点の間隔に注目して考えるのか、どちらが良いだろうか？
• 点に注目した場合、書き出して整理する形に近くなるな。これでも解けそうだ。モレとダブりの防ぎ方がポイントだな。
• 点と点の間隔に注目した場合、組み合わせとして構造的にアプローチできそうだ。モレとダブりもしっかり注意できそうだ。

よし、今回は点と点の間隔に注目して、より構造的にアプローチしてみよう！

ここでは方針の検討をしっかり行います。

4.構造的にアプローチする。
（抜け•漏れ•ダブりを防ぎ、原因と結果の関係に注目し、理屈の構造を明らかにする。）

• 点と点の間隔が合計12個あり、頂点と頂点の間には3つ以上の間隔がある必要がある。これが成立の必須条件だ。
• となると、各頂点の間隔の組み合わせは以下のように3パターン（順不同）が考えられる。

1. (パターン1)  3 - 3 - 6 (合計12)  ←直径を通る直角二等辺三角形
2. (パターン2)  3 - 4 - 5 (合計12)  ←普通の？三角形
3. (パターン3)  4 - 4 - 4 (合計12)  ←正三角形

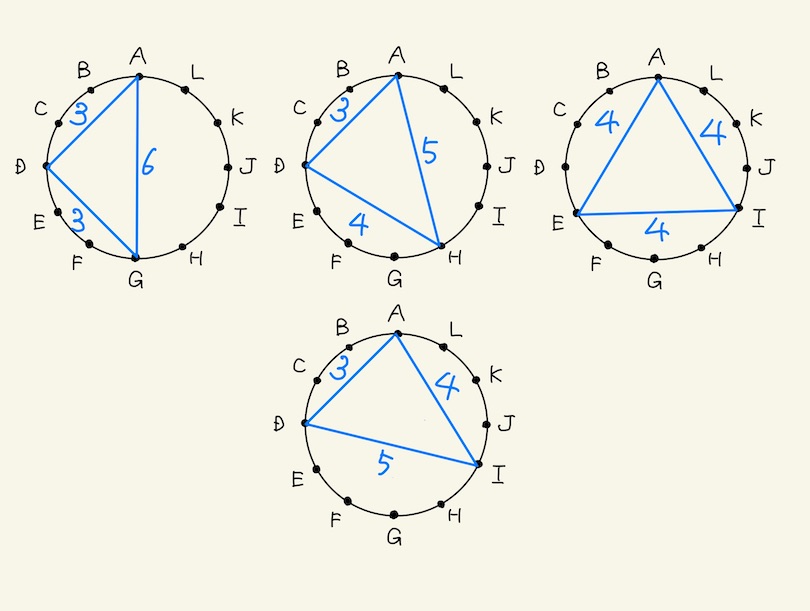
• 3パターンそれぞれの場合の数を数えよう。

1. (パターン1)  3 - 3 - 6 (合計12)  ←直径を通る直角二等辺三角形
   直角の頂点がA〜Lの12種類とれる。
2. (パターン2)  3 - 4 - 5 (合計12)  ←普通の？三角形
   【注意】
   3-4-5 と 3-5-4 の2種類は異なる三角形である！（※3-4-5と4-5-3,5-3-4は同じ。3-5-4と5-4-3,4-3-5は同じ。）
   例えば、△AJF（3-4-5）と△AJE（3-5-4）は異なる三角形である。
   よって、AJの辺の取り方に注目すると、12種類ある。そして、それぞれに3-4-5と3-5-42パターンがあるので。
   12×2=24種類とれる。
3. (パターン3)  4 - 4 - 4 (合計12)  ←正三角形
   4種類とれる。（※12÷3=4）

以上より、

12 + 24 + 4 = 40個

5.問い続ける。
（出た結論に対して「なぜ？」「だから？」「本当に？」と問い続けて見落としや新たな発見につなげる。）

【別解】

点に注目して考えてみる。仮にAから始まるとして、異なる三角形の形の種類を洗い出してみると、

A - D - G、H、I、J    の4種類
A - E - H、I、J    の3種類
A - F - I、J     の2種類
A - G - J     の1種類

10種類となる。

A〜Lの12個の点があるので、10×12=120種類となる。

しかし、例えば、点Aから数えた△ADGは、点Dから数えた△DGAと点Gから数えた△GADとダブる。

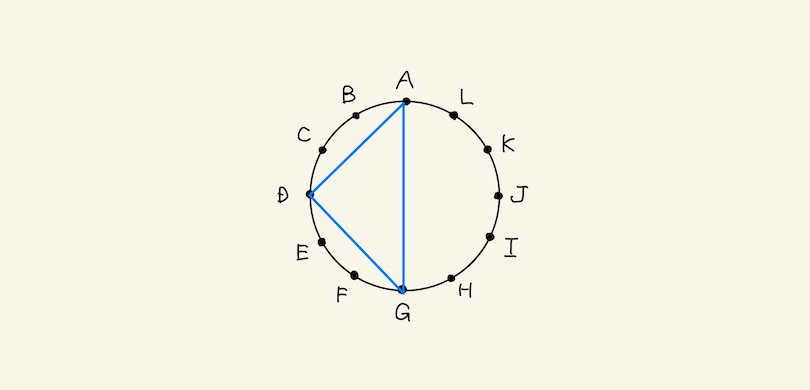
よって、10 × 12 ÷ 3 = 40個　となる。

以上。

上記の解説より、

• 点と点の間隔が合計12個あり、頂点と頂点の間には3つ以上の間隔がある必要がある。
• となると、各頂点の間隔の組み合わせは以下のように3パターン（順不同）が考えられる。

1. (パターン1)  3 - 3 - 6 (合計12)  ←直径を通る直角二等辺三角形
2. (パターン2)  3 - 4 - 5 (合計12)  ←普通の？三角形
3. (パターン3)  4 - 4 - 4 (合計12)  ←正三角形

• 3パターンそれぞれの場合の数を数える。

1. (パターン1)  3 - 3 - 6 (合計12)  ←直径を通る直角二等辺三角形
   直角の頂点がA〜Lの12種類とれる。
2. (パターン2)  3 - 4 - 5 (合計12)  ←普通の？三角形
   【注意】
   3-4-5 と 3-5-4 の2種類は異なる三角形である！
   例えば、△AJF（3-4-5）と△AJE（3-5-4）は異なる三角形である。
   よって、AJの辺の取り方に注目すると、12種類ある。そして、それぞれに3-4-5と3-5-42パターンがあるので。
   12×2=24種類とれる。
3. (パターン3)  4 - 4 - 4 (合計12)  ←正三角形
   4種類とれる。（※12÷3=4）

よって、12 + 24 + 4 = 40個

以上。

• モレなくダブりなく数えるために、自分自身のルールをしっかり作り、守ること。
• なるべく、シンプルなルールを作ること。
• 大分類にうまく場合分けして、その大分類の中をさらに絞り込んでいく方が良い場合も多いので、そういった経験値を持っておく。（※公式だけで一気に解こうとしない。）